Summary:
- You started with an investment of:$ on
- Your principal amount grew to:$ by
- Your total cash withdrawals were: $ over the course of business days
- Your total NET profit for the -day period was: $
Projection breakdown
Download your result
| Day | Date | Earnings | Reinvest | (Principal/Cash Out) | TOTAL Principal | TOTAL Cash |
|---|
Table of Contents
Understanding the Compound Interest Formula and Building Long-Term Wealth
Compound interest is a fundamental concept in finance that can transform modest savings into substantial wealth over time. It’s the process of earning interest on your initial investment, as well as on the interest accumulated from previous periods. This article will delve into the compound interest formula, its implications for long-term wealth building, and how utilizing an online compound interest calculator can significantly aid in managing and growing your investment portfolio.
The Essence of Compound Interest
At its core, compound interest is interest calculated on the initial principal, which also includes all the accumulated interest from previous periods. Unlike simple interest, where interest is only calculated on the principal amount, compound interest allows your investment to grow at an accelerated rate.
The formula for compound interest is:
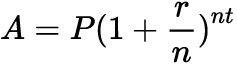
Where:
- A is the future value of the investment/loan, including interest.
- P is the principal investment amount.
- r is the annual interest rate (decimal).
- n is the number of times that interest is compounded per year.
- t is the time the money is invested or borrowed for, in years.
This formula is powerful because it shows how your investments grow exponentially over time, as the interest you earn each period is added to your principal, forming a new base for future interest calculations.
Impact of Compound Interest on Long-Term Wealth
The true power of compound interest manifests in long-term investments. The longer your money compounds, the more substantial the growth. This effect is particularly noticeable over periods of several decades, making it a cornerstone strategy for retirement savings and long-term financial planning.
For instance, if you start with a principal amount and let it grow through compound interest, the accumulated amount after several years can be significantly higher than the original investment. This exponential growth is what makes compound interest a potent tool for building wealth over time.
It’s crucial to start early, as the time factor plays a pivotal role in maximizing the benefits of compound interest. Even with smaller initial investments, the compounding effect over many years can lead to impressive financial gains.
Utilizing an Online Compound Interest Calculator
An online compound interest calculator simplifies the process of understanding and applying the compound interest formula to your investment decisions. It allows you to input different variables, including the principal amount, interest rate, compounding frequency, and investment duration, to instantly see the potential growth of your investments.
This tool is invaluable for planning and optimizing your long-term investment strategy. It helps you:
- Visualize Investment Growth: By inputting different scenarios, you can see how small changes in the interest rate or investment duration can significantly impact your returns.
- Plan Financial Goals: Set realistic and informed financial goals based on the calculated potential growth of your investments.
- Compare Investment Options: Experiment with various rates and timeframes to determine the most suitable investment strategies for your goals.
- Stay Motivated and Focused: Regularly using the calculator to track the potential growth of your investments can be a motivating factor in maintaining and increasing your savings rate.
Moreover, the ability to download the calculated results in PDF or XLS formats makes it easier to keep a record of your financial plans and track your progress towards your investment goals.
Building and Managing Your Investment Portfolio with Compound Interest
Incorporating compound interest into your investment strategy requires a disciplined and long-term approach. Start by allocating a consistent portion of your income towards investments. Diversify your portfolio to include assets with varying levels of risk and potential return, such as stocks, bonds, and mutual funds.
Regularly use the online compound interest calculator to reassess your investments. It can provide insights into how changing market conditions and interest rates affect your portfolio’s growth potential. This practice encourages a proactive approach to portfolio management, ensuring your investments align with your financial objectives.
Remember, the key to benefiting from compound interest is patience and consistency. Avoid the temptation to withdraw your investments early. The longer your money stays invested, the more significant the compounding effect.
The compound interest formula is more than just a mathematical equation; it’s a roadmap to financial freedom and long-term wealth. By understanding and applying this formula through disciplined investing and the use of an online compound interest calculator, you can effectively plan, manage, and grow your investment portfolio. Embrace the power of compound interest, and watch as your financial goals become a tangible reality.
